В работе М.Ф. Маликова «Основы метрологии» отмечено, что по происхождению систематические ошибки принято разделять на несколько категорий.
Инструментальные ошибки обусловлены конструктивными недостатками применяемой аппаратуры, ее неисправностью или неправильной градуировкой.
Ошибки установки возникают вследствие неправильной или небрежной установки или расположения измерительной аппаратуры.
Личные ошибки обусловлены индивидуальными особенностями аналитика (например, личные ошибки в определении равенства интенсивностей линии при работе со стиллоскопом).
Ошибки метода, а также теоретические ошибки связаны с недостаточным знанием или неполным учетом всех обстоятельств, влияющих на правильность результатов. Последняя разновидность ошибок в практике спектрального анализа обычно является наиболее существенной (ошибки, обусловленные влиянием третьих элементов, минералогического состава и т.п. факторов).
При рассмотрении вопроса о случайных ошибках спектрального анализа необходимо условно принять, сто систематические ошибки исключены. Только с этой оговоркой можно считать в качестве наиболее достоверной характеристики содержание элементов в анализируемой пробе среднее арифметическое результатов параллельных определений. В противном случае центр рассеяния результатов смещается и вычисленное среднее, например, x1 оказывается «сдвинутым» относительно содержания, принимаемого за достоверное, x2.
Таким образом, вычисленный из ряда параллельных определений средний результат при наличии систематической ошибки может служить только основой для вычисления разброса данных, но не для характеристик содержания анализируемого компонента. Отсюда очевидная важность контроля и профилактики появления систематических ошибок в результатах определений.
Чаще всего систематические ошибки спектрального анализа обнаруживаются вследствие того, что результаты определений, выполненных в разных условиях (например, при использовании разных по композиции комплектов эталонов, существенно различных методов анализа), не совпадают.
Если подобные расхождения велики и превосходят случайные отклонения, то наличие систематических ошибок, по крайней мере в результатах одной из сравниваемых серий определений, не вызывает сомнений.
Более сложным для исследования является случай, когда систематические ошибки — одного порядка с величинами случайных ошибок.
Естественно, что не во всех перечисленных случаях систематические ошибки опасны в одинаковой мере, однако требования к их исключению является жесткими.
Достаточным критерием ограничения систематических ошибок было бы выполнение условия
εсист < 0,5 τp
где τp — средняя квадратическая ошибка результата анализа.
Однако в практике применения спектрального анализа, как и во многих других случаях технических измерений, в частности при использовании химических методов анализа, далеко не всегда удается удовлетворить этому критерию. Важно, однако, подчеркнуть, что необходимость исключения или учета систематических ошибок должна находиться в поле зрения аналитика в той же степени, как и необходимость уменьшения случайных ошибок.
В большинстве случаев для решения этой задачи необходимы постановка специальных экспериментов и тщательный анализ опытных данных, основанные на хорошем знании всей совокупности вопросов, относящихся к рассматриваемой задаче.
Обнаружение систематических расхождений в спектральном анализе
- Для оценки правильности результатов применения спектрального анализа прибегают к ряду приемов:
- анализы выполняют с помощью стандартных образцов и синтетических эталонов,
- контролируют по сумме содержаний,
- путем введения известных добавок и т.д.
Во всех подобных случаях систематическая ошибка обнаруживается лишь по наличию существенного систематического расхождения между сопоставляемыми результатами (например, между средними результатами, которые получены разными методами, или между суммой процентных содержаний всех элементов в образце и 100% и т.д.). Поэтому первоочередной задачей в этих случаях является надежное установление факта существенного систематического расхождения. Такой факт устанавливается наиболее просто, если расхождения значительно превышают возможную случайную ошибку результата сравнения сопоставляемых данных (о ее вычислении — см. далее).
Часто, однако, имеет место наслоение случайных и систематических ошибок , являющихся величинами одного порядка, и тогда необходим более подробный анализ опытных данных. Решение задач подобного типа основано на следующих соображениях.
Общий случай
Если две серии определений характеризуются средними квадратичными ошибками единичного определения (СКОед) s1 и s1, то ошибки результатов средних x1 и x2, из n1 и n2 определений будут соответственно
sp,1 = s1 ⁄ √ n1 и sp,2 = s2 ⁄ √ n2
где s1 и s2 — СКОед каждой серии измерений, n1 и n2 — количество измерений в каждой серии.
Требуется выяснить, является ли различие величин x1 и x2 случайным или же оно обусловлено наличием систематических ошибок.
В теории измерений показывается, что если значения x1 и x2 установлены с ошибками sp,1 и sp,2, то ошибка разности |x1 − x2| составит
sp = √ s2p,1 + s2p,2
Наибольшая практически возможная случайная ошибка результата сравнения в спектральном анализе составляет (по правилу «трех сигм») 3 sp, т.е. если
|x1 − x2| > 3 sp
то можно с уверенностью утверждать, что различие величин x1 и x2 не может быть объяснено действием случайных факторов. Надежность такого заключения — около 100%, т.е. делая это заключение, можно полагать с вероятностью близкой к единице, что оно достоверно. Если задаться меньшей надежностью, например принять доверительную вероятность равной 0,95, то формула (1) превратится:
|x1 − x2| > 2 sp
Надежность этого заключения — около 95%, так как в «двухсигмовые» пределы укладывается уже не 100% всех ошибок, а лишь 95%. В этом случае не исключена возможность, что расхождение, численно превышающее 2 sp, будет принято за реально существующее, в то время как оно обусловлено появлением случайной ошибки, больше 2 sp. Вероятность такого случая составляет 1,00−0,95=0,05.
Конечно, если соотношения (1) и (2) не выполняются, т.е., например |x1 − x2| < 3 sp или |x1 − x2| < 2 sp , то это не означает, что систематическое расхождение полностью отсутствует. В этом случае нельзя лишь определенно утверждать (для данной доверительной вероятности), чем вызвано различие величин x1 и x2 — действием случайных факторов или неисключенными полностью систематическими отклонениями.
Часто возникает обратная задача: если все же утверждать, что различие |x1 − x2| имеет место, то какова надежность такого заключения.
Для решения этой задачи следует обратить внимание на то, что в формулах (1) и (2) коэффициент перед sp характеризует надежность вывода о наличии расхождения : для доверительной вероятности около 1,0 этот коэффициент равен трем, для доверительной вероятности 0,95 — двум и т.д. Поэтому исходя из формулы (1) или (2) можно составить выражение
| |x1 − x2| | = t |
| sp |
где t — коэффициент перед sp в соотношениях типа (1) или (2), и по величине t определить доверительную вероятность.
| t | 1,0 | 1,3 | 1,6 | 2,0 | 2,3 | 2,6 |
|---|---|---|---|---|---|---|
| Доверительная вероятность | 0,70 | 0,80 | 0,90 | 0,95 | 0,98 | 0,99 |
Так, например, если t=1,80, то можно утверждать с вероятностью 0,95 и выше, что различие величин x1 и x2 находится в пределах возможной ошибки, а с вероятностью 0,90 — что оно превышает эту ошибку.
Малые выборки
Приведенные заключения справедливы, если величины, входящие в выражение (3) вычислены по достаточно большому количеству измерений. Если обрабатывается малое число наблюдений, то значение величин, входящих в формулу (3) находят по формулам, приведенным в соответствующих работах по математический статистике.
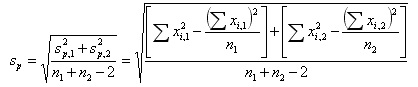
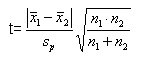
где x1,i и x2,i — результаты единичных определений в сериях, для которых вычислялись значения x1 и x2.
В формуле (4) использован упрощенный прием вычисления и в соответствии с формулой (6).
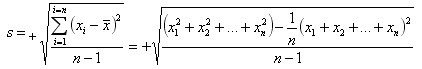
Для малого числа измерений пользуются таблицей 2, в которой зависимость между t и доверительной вероятностью откорректирована с учетом неопределенности, вносимой ограниченным числом наблюдений.
Легко видеть, что последняя строка значений в табл. 2 для (n1 + n2 — 2) > 20 совпадает с данными табл. 1
Значения t в зависимости от числа наблюдений n1 и n2 для различной доверительной вероятности |
||||||
|---|---|---|---|---|---|---|
Число наблюдений n1 + n2 - 2 |
Доверительная вероятность | |||||
| 0,70 | 0,80 | 0,90 | 0,95 | 0,98 | 0,99 | |
| 1 | 2,0 | 3,1 | 6,3 | 12,7 | 31,8 | 63,7 |
| 2 | 1,3 | 2,9 | 2,9 | 4,3 | 7,0 | 9,9 |
| 3 | 1,2 | 2,6 | 2,4 | 3,2 | 4,5 | 5,8 |
| 4 | 1,2 | 1,5 | 2,1 | 2,8 | 3,8 | 4,6 |
| 5 | 1,2 | 1,5 | 2,0 | 2,6 | 3,4 | 4,0 |
| 10 | 1,1 | 1,4 | 1,8 | 2,2 | 2,8 | 3,2 |
| 20 | 1,1 | 1,3 | 1,7 | 2,1 | 2,5 | 2,8 |
| >20 | 1,0 | 1,3 | 1,6 | 2,0 | 2,3 | 2,6 |

















