Как видно из формул (1) - (3) влияние колебаний температуры в разряде на интенсивность линий спектров является особенно сильным, т.к. температура является аргументом экспоненциальной функции.
Для того, чтобы минимизировать это влияние в атомно-эмиссионном спектральном анализе (АЭСА) применяют специальный прием. Он заключается в том, что для каждой аналитической спектральной линии определяемого элемента подбирают еще одну спектральную линию другого элемента (часто называемого внутренним стандартом) с равным или близким потенциалом возбуждения. При этом в качестве аналитического сигнала берется не интенсивность аналитической линии определяемого элемента, а отношение интенсивности аналитической линии определяемого элемента и интенсивности спектральной линии внутреннего стандарта с равным или близким потенциалом возбуждения:
(4)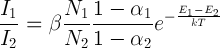
где постоянная 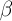 содержит статические веса состояний, вероятности излучения и длины волн, индексы 1 и 2 обозначают величины, относящиеся к аналитической линии определяемого элемента и спектральной линии внутреннего стандарта, соответственно.
содержит статические веса состояний, вероятности излучения и длины волн, индексы 1 и 2 обозначают величины, относящиеся к аналитической линии определяемого элемента и спектральной линии внутреннего стандарта, соответственно.
При одинаковых или близких потенциалах возбуждения 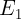 и
и 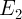 экспоненциальный множитель в формуле (4) становится равным или близким к единице, что и минимизирует влияние температуры.
экспоненциальный множитель в формуле (4) становится равным или близким к единице, что и минимизирует влияние температуры.
Пары линий с равными или близкими потенциалами возбуждения, применяемые для анализа, называются аналитическими гомологическими линиями или аналитическими парами линий. Очень часто спектральную линию внутреннего стандарта, входящую в аналитическую пару, называют линией сравнения.
В идеале желательно, чтобы атомы элементов, линии которых входят в аналитическую пару, имели бы еще и близкие потенциалы ионизации, что обеспечило бы еще и близкие значения степеней ионизации 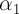 и
и 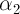 .
.
Из формулы (4) видно, что аналитический сигнал в виде отношения интенсивностей аналитической линии и линии сравнения пропорционален отношению концентраций анализируемых атомов и атомов внутреннего стандарта. Часто аналитический сигнал в виде отношения интенсивностей аналитической линии и линии сравнения называют относительной интенсивностью, а отношение концентраций анализируемых атомов и атомов внутреннего стандарта — относительной концентрацией.
При таком подходе и связь между концентрацией 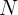 анализируемого химического элемента в плазме от его концентрации в анализируемой пробе
анализируемого химического элемента в плазме от его концентрации в анализируемой пробе 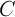 в этом случае ищут в виде функции, связывающей соответствующие относительные концентрации:
в этом случае ищут в виде функции, связывающей соответствующие относительные концентрации: 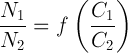
Понятно, что в этом случае градуировочные характеристики связывают между собой относительные интенсивности (аналитической линии и линии сравнения) и относительные концентрации (атомов анализируемого химического элемента и атомов внутреннего стандарта) в анализируемой пробе:
(5)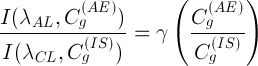
или на практике более удобной является обратная зависимость:
(6)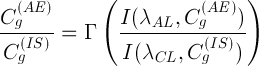
(Здесь 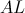 — аналитическая линия (analytical line),
— аналитическая линия (analytical line),
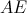 — анализируемый элемент (analyzed element),
— анализируемый элемент (analyzed element),
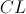 — линия сравнения (comparison line),
— линия сравнения (comparison line),
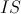 — внутренний стандарт (internal standard),
индекс
— внутренний стандарт (internal standard),
индекс 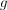 нумерует стандартные образцы в комплекте, предназначенном для построения ГХ).
нумерует стандартные образцы в комплекте, предназначенном для построения ГХ).
Из формул (5) и (6) сразу понятно, что при применении описанного подхода, т.е. для получения значения концентрации анализируемого элемента 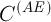 в пробе необходимо знать концентрации элемента внутреннего стандарта как в градуировочных стандартных образцах
в пробе необходимо знать концентрации элемента внутреннего стандарта как в градуировочных стандартных образцах 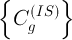 , так и в самой анализируемой пробе.
, так и в самой анализируемой пробе.
Естественно возникает вопрос о том, как выбрать элемент внутренний стандарт, если элементный состав анализируемой пробы заранее неизвестен и подходящего (по соображениям близости потенциалов возбуждения) элемента внутреннего стандарта там может и вовсе не быть?
В процессе развития АЭСА выработано два подхода к решению этого вопроса.
Первый применяется в случае, когда исходный анализируемый образец подвергается процессу пробоподготовки. Например, в случае ИСП-спектрометров исходная твердая проба подвергается химическому растворению и превращается в жидкий раствор. Во время этой процедуры в растворенный образец можно добавить известное количество подходящего элемента внутреннего стандарта, при условии, что его не было в составе исходного образца. Таким образом, концентрация внутреннего стандарта оказывается известной по процедуре приготовления.
Этот подход не годится в тех случаях, когда агрегатное состояние исходного анализируемого образца в процессе анализа не меняется, например, при спектральном экспресс-анализе металлов и сплавов в виде твердых монолитов на искровых спектрометрах. Но в этом случае основу таких проб всегда составляет один элемент (реже несколько элементов) с очень большой концентрацией, т.н. матричный элемент или основа. Например, в сталях и чугунах матричным элементом является железо, в бронзах и латунях — медь, и т.д. Причем в подавляющем большинстве аналитических приложений требуется определять концентрации примесных элементов, а не матричного.
Здесь, прежде чем двигаться дальше, сделаем небольшое разъяснение.
Особенности и разъяснения
До сих пор везде мы применяли термин концентрация атомов (или ионов) элемента (т.е. число соответствующих частиц в единице объема), т.к. интенсивность спектральных линий в разряде зависит именно от этой физической величины. Но оперировать концентрациями атомов (или ионов) элемента для целей анализа состава пробы крайне не удобно. Во-первых, потому, что это очень большие числа (например, при 1%-м содержании углерода в стали число атомов углерода в кубическом сантиметре равно примерно 4⋅1021). Во-вторых, результатом анализа является выяснение количества того или иного вещества (химического элемента) в составе данного образца, которое обычно выражается в единицах массы (г или кг). Но абсолютное значение массы данного элемента в данной пробе также не показательно, т.к. оно зависит от массы пробы. Чтобы избежать этого используют понятие массовой доли элемента в образце.
Массовая доля элемента представляет собой отношение массы данного химического элемента в пробе к массе этой пробы.
Массовая доля — безразмерная величина и чаще всего выражается в % (иногда уточняют: масс. %), или в других часто используемых долевых единицах, таких как ppm (part per million — одна миллионная часть), или ppb (part per billion — одна миллиардная часть), или г/т. Очевидно, что
1 ppm = 1 г/т = 10-4 % = 1000 ppb.
Иногда при анализах жидких проб содержание элемента выражают в мг/л. Хотя содержание в этих единицах выглядит размерной величиной, на самом деле оно остается безразмерным, т.к. подразумевается водный раствор, а масса 1 литра воды равна 1 кг. Поэтому 1 мг/л = 1 ppm.
Величина, пропорциональная концентрации, но выражаемая в массовых долях, называется содержанием элемента в образце. Соответственно, во всех вышеуказанных формулах под величинами концентраций 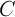 можно подразумевать содержание элемента в образце, выраженное в массовых долях.
можно подразумевать содержание элемента в образце, выраженное в массовых долях.
Вернемся теперь к обсуждению выбора элемента внутреннего стандарта при анализе состава образцов металлов и сплавов в виде твердых монолитов на искровых спектрометрах.
В этом случае в качестве элемента внутреннего стандарта выбирается матричный элемент (Fe в случае сталей, Cu в случае сплавов меди и т.д.). Соответственно для каждой аналитической линии 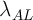 определяемого элемента подбирается линия сравнения
определяемого элемента подбирается линия сравнения 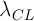 — подходящая по близости потенциала возбуждения спектральная линия матричного элемента.
Далее для каждого стандартного образца (нумеруемых ниже индексом
— подходящая по близости потенциала возбуждения спектральная линия матричного элемента.
Далее для каждого стандартного образца (нумеруемых ниже индексом 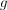 ) производятся измерения интенсивностей аналитической линии
) производятся измерения интенсивностей аналитической линии 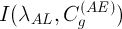 и линии сравнения
и линии сравнения 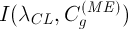 и образуется массив точек с координатами
и образуется массив точек с координатами
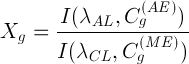 и
и 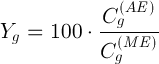
(коэффициент 100 появляется при отсчетах относительных содержаний 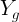 в %). Количество точек равно количеству стандартных образцов.
в %). Количество точек равно количеству стандартных образцов.
Напомним, что содержания анализируемых элементов 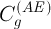 в стандартных образцах заранее известны. А содержания матричного элемента в
в стандартных образцах заранее известны. А содержания матричного элемента в 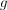 -том стандартном образце определяются из того факта, что сумма содержаний (в масс. %) всех элементов равна 100%:
-том стандартном образце определяются из того факта, что сумма содержаний (в масс. %) всех элементов равна 100%:
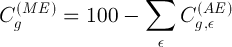
где целый индекс  нумерует анализируемые элементы в
нумерует анализируемые элементы в 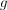 -том стандартном образце.
-том стандартном образце.
Затем строится (например, методом наименьших квадратов) градуировочная характеристика в виде функции 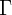 , проходящей через или вблизи точек массива и связывающей относительные интенсивности и относительные содержания (в %):
, проходящей через или вблизи точек массива и связывающей относительные интенсивности и относительные содержания (в %):
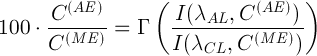
Применяя в дальнейшем эту градуировочную характеристику для определения неизвестных содержаний элементов в анализируемой пробе по результатам измерения относительных интенсивностей 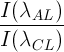 , получаем значения относительных содержаний
, получаем значения относительных содержаний 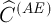 (в %) в ней:
(в %) в ней:
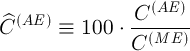
Но результатом анализа пробы должны быть не относительные содержания элементов в ней, а абсолютные, т.е. значения 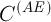 . А как их найти, если для анализируемой пробы содержание матричного элемента
. А как их найти, если для анализируемой пробы содержание матричного элемента 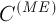 неизвестно?
неизвестно?
Из формулы (9) находим:
(10)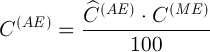
Просуммируем (10) по всем анализируемым элементам:
(11)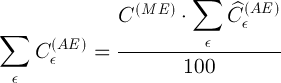
где целый индекс  нумерует анализируемые элементы в пробе.
нумерует анализируемые элементы в пробе.
Вспомнив, что 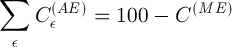 , из (10) и (11) получаем:
, из (10) и (11) получаем:
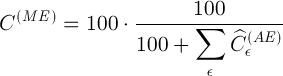
и искомое значение абсолютного содержания определяемого элемента в пробе:
(13)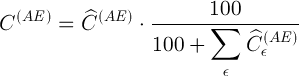
Таким образом, для перехода от измеренного (в %) относительного содержания элемента в пробе к искомому абсолютному содержанию (в масс. %) необходимо знать сумму относительных содержаний (в %) всех элементов, присутствующих в пробе, кроме матричного.
Часто встречается более сложная ситуация, когда методом атомно-эмиссионного спектрального анализа определяются не все присутствующие в пробе элементы, а лишь их часть. Соответственно, данные по другим элементам либо известны заранее, либо получены при анализе той же пробы другими методами (например, химическими). В этом случае формулы (12) и (13) приобретают вид:
(14)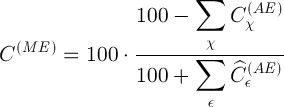
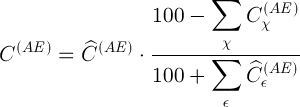
где целый индекс 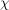 нумерует анализируемые элементы в пробе, содержание которых (в масс. %) определены другими методами. Читать дальше ›
нумерует анализируемые элементы в пробе, содержание которых (в масс. %) определены другими методами. Читать дальше ›

















