Построение градуировочных характеристик и их влияние

Авторы:

сотрудники компании

Часть 1. Введение. Применимость для неразрушающего контроля. Принципы Часть 2. Плазма – наиболее распространенный источник возбуждения спектров Часть 3. О связи интенсивности спектральных линий с концентрацией (или содержанием) анализируемого элемента в пробе Часть 4. О градуировании (или калибровке) по стандартным образцам для количественного спектрального анализа Часть 5. О внутреннем стандарте и линиях сравнения Часть 6. О влияниях. Построение градуировочных характеристик

Обсудим теперь еще одну особенность атомно-эмиссионного спектрального анализа, определяемую терминами «матричные влияния» или «влияния основы» или «межэлементные влияния».

Суть этой особенности в том, что во многих случаях значение аналитического сигнала и результат анализа оказываются зависимыми не только от относительного содержания определяемого элемента, но и от содержания остальных элементов (в том числе и матричного), фазового состава и микроструктуры анализируемых образцов.

Физическая природа матричных эффектов весьма многообразна и поэтому до сих пор для них нет каких-либо единых аналитических соотношений. На практике с целью минимизации искажения получаемых результатов анализа из-за матричных эффектов стремятся к максимально возможному сближению состава и свойств анализируемых проб и применяемых для градуирования спектрометров стандартных образцов, включая в том числе и такие факторы, как структура материала, масса, форма и размеры образцов и т.д.

Одним из признаков проявления матричных эффектов является тот факт, что градуировочные точки, то есть точки с координатами
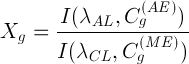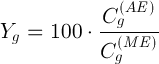$X_g=\frac{I(\lambda_{AL},C_g^{(AE)})}{I(\lambda_{CL},C_g^{(ME)})}$ и $Y_g=100\cdot \frac{C_g^{(AE)}}{C_g^{(ME)}}$ сильно «скачут», т.е. не ложатся на монотонную кривую. Другими словами, не удается построить монотонную градуировочную функцию, проходящую около точек с координатами
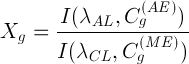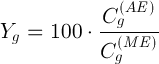$X_g=\frac{I(\lambda_{AL},C_g^{(AE)})}{I(\lambda_{CL},C_g^{(ME)})}$ и $Y_g=100\cdot \frac{C_g^{(AE)}}{C_g^{(ME)}}$ в пределах погрешностей этих точек.

В настоящее время наиболее распространен достаточно формальный метод учета матричных эффектов, заключающийся в коррекции исходной градуировочной характеристики путем введения дополнительных параметров.

Этот метод условно подразделяет все матричные эффекты на два типа:

аддитивные, смещающие исходную градуировочную характеристику параллельно самой себе в зависимости от содержания влияющего элемента,
и мультипликативные, приводящие к изменению угла наклона градуировочной характеристики относительно координатных осей также в зависимости от содержания влияющего элемента.

Прежде чем продолжить описание метода учета матричных эффектов, сделаем небольшое отступление и опишем наиболее распространенный подход к построению градуировочных характеристик.

Построение градуировочных характеристик

Чаще всего градуировочная характеристика для данной аналитической пары (аналитическая линия 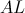$AL$ /линия сравнения 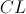$CL$ ) ищется в виде полинома 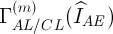$\Gamma_{AL/CL}^{(m)}(\widehat{I}_{AE})$ степени 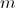$m$ вида:

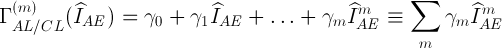
(16) $\Gamma_{AL/CL}^{(m)}(\widehat{I}_{AE})=\gamma_0+\gamma_1\widehat{I}_{AE}+\ldots+\gamma_m\widehat{I}_{AE}^m\equiv \sum_m\gamma_m\widehat{I}_{AE}^m$

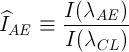где $\widehat{I}_{AE}\equiv\frac{I(\lambda_{AE})}{I(\lambda_{CL})}$ — измеренное значение относительных интенсивностей аналитической линии анализируемого элемента и линии сравнения внутреннего стандарта, 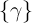$\left\{\gamma\right\}$ — искомые коэффициенты. Очевидно, что величина степени полинома 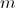$m$ не может превосходить числа градуировочных стандартных образцов, уменьшенного на единицу.

Часто в качестве 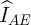$\widehat{I}_{AE}$ берут не относительную интенсивность, а ее логарифм. Иногда градуировочная характеристика ищется не виде (16), т.е. полинома по степеням относительной интенсивности (или ее логарифма), а в виде отрезка ряда по полиномам Чебышева (поскольку именно эти полиномы наиболее адекватны применяемому в последующем методу наименьших квадратов).

Коэффициенты 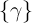$\left\{\gamma\right\}$ ищут тем или иным регрессионным методом, например, методом наименьших квадратов. Суть этого метода в том, что искомые коэффициенты 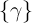$\left\{\gamma\right\}$ должны быть такими, чтобы сумма квадратов отклонений содержаний элемента в градуировочных образцах от искомой градуировочной характеристики была минимальной:

(17) $Q_{AL/CL}\equiv\sum_g\left [\frac{\widehat{C}_g^{AE}-\Gamma_{AL/CL}^{(m)}(\widehat{I}_{AE})}{\delta \widehat{C}_g^{AE}}\right ]^2=min$

Где суммирование ведется по градуировочным стандартным образцам, 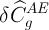$\delta \widehat{C}_g^{AE}$ — погрешность относительного содержания анализируемого элемента в g-том стандартном образце. Величины 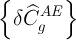$\left\{\delta\widehat{C}_g^{AE}\right\}$ известны из документации на стандартные образцы.

Условие достижения минимума известно — равенство нулю частных производных:

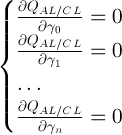
(18) $\begin{cases} \frac{\partial Q_{AL/CL}}{\partial\gamma_0} =0 \\ \frac{\partial Q_{AL/CL}}{\partial\gamma_1} = 0 \\ \ldots \\ \frac{\partial Q_{AL/CL}}{\partial\gamma_n} = 0 \end{cases} \right$

Совокупность уравнений (18) образует систему линейных уравнений относительно искомых коэффициентов 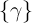$\left\{\gamma\right\}$ , которые и находятся применением какого-либо метода решения таких систем.

Вернемся к обсуждению метода учета матричных эффектов.

Первый тип влияний — аддитивный, учитывают введением в исходную формулу (16) для исходной градуировочной характеристики данного анализируемого элемента дополнительных слагаемых, пропорциональных измеренным относительным интенсивностям остальных элементов образца:

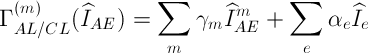
(19) $\Gamma_{AL/CL}^{(m)}(\widehat{I}_{AE})=\sum_m\gamma_m\widehat{I}_{AE}^m+\sum_e\alpha_e\widehat{I}_e$

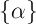где индекс $_e$ нумерует остальные элементы образца, которые принимаются аналитиком в качестве влияющих факторов. Это может быть один или несколько остальных элементов, но не обязательно все остальные элементы. Коэффициенты $\left\{\alpha\right\}$ также вычисляются регрессионным методом.

Второй тип влияний — мультипликативный, описывается разворотом градуировочной характеристики и учитывается домножением скорректированной на аддитивные влияния градуировочной функции (19) на соответствующий множитель:

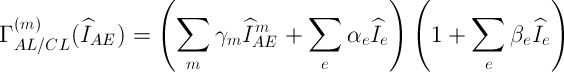
(20) $\Gamma_{AL/CL}^{(m)}(\widehat{I}_{AE})=\left( \sum_m\gamma_m\widehat{I}_{AE}^m+\sum_e\alpha_e\widehat{I}_e\right)\left( 1+\sum_e\beta_e\widehat{I}_e \right)$

Коэффициенты 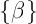$\left\{\beta\right\}$ вычисляются опять таки регрессионным методом.

Еще раз повторим, что описанный подход к учету межэлементных влияний является формальным, т.к. не отвечает на вопрос в каком случае и какие конкретно элементы в образцах следует включать в формулу (20) в качестве влияющих. Чисто формальное введение в формулу (20) влияющих факторов (якобы влияющих!), не подкрепленное серьезными соображениями, является подгонкой и потому недопустимо.

Конечно, если имеются какие-либо физические соображения или модели, из которых можно сделать заключение о влиянии одного элемента на другой, то они помогают определиться с перечнем влияющих элементов в формуле (20). Здесь большую роль играет аналитический опыт и эрудиция оператора. Во многих случаях навести на мысль о влиянии того или иного элемента на анализируемый элемент помогает вычисление коэффициентов корреляции 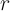$r$ для каждого градуировочного образца:

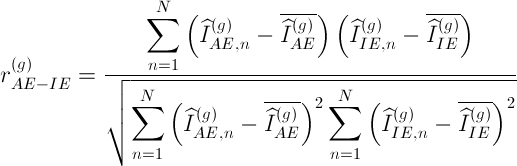
(21) $r_{AE-IE}^{(g)} = \frac { \displaystyle{\sum_{n=1}^N} \left( \widehat{I}_{AE, n}^{(g)}-\overline{\widehat{I}_{AE}^{(g)}} \right) \left( \widehat{I}_{IE, n}^{(g)}-\overline{\widehat{I}_{IE}^{(g)}} \right) } { \sqrt { \displaystyle{\sum_{n=1}^N} \left( \widehat{I}_{AE, n}^{(g)}-\overline{\widehat{I}_{AE}^{(g)}} \right)^2 \displaystyle{\sum_{n=1}^N} \left( \widehat{I}_{IE, n}^{(g)}-\overline{\widehat{I}_{IE}^{(g)}} \right)^2 } }$

где индекс 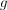$_g$ — нумерует градуировочный стандартный образец, 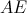$AE$ — обозначает анализируемый элемент (analyzed element),
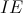$IE$ — обозначает влияющий элемент (influencing element), 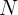$N$ — число параллельных измерений соответствующих относительных интенсивностей, 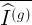$\widehat{I}^{(g)}$ — среднее арифметическое:

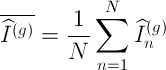
$\overline{\widehat{I}^{(g)}}=\frac{1}{N}\sum_{n=1}^{N}\widehat{I}_n^{(g)}$

Если модуль коэффициента корреляции 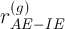$r_{AE-IE}^{(g)}$ оказывается близок к 1, то это может служить основанием для заключения о возможности влияния элемента 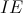$IE$ на анализируемый элемент 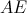$AE$ в данном градуировочном образце. Очень важным при вычислениях коэффициента корреляции является достаточно большое число параллельных измерений, — не менее 10 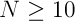$N\geq 10$ . Следует также отчетливо понимать, что наличие обнаруженной корреляционной связи еще не дает основания однозначно утверждать, что имеет место именно влияние одного элемента на другой. Возможно, что наличие этой связи указывает на действие еще одного, третьего, неизвестного фактора. Опять таки нужны дополнительные физические соображения.